xe^x的点数主要包括不定点数和定点数。不定点数求的是表达式f(x)=xe^x的原表达式，能记作F(x)+C，它是两个表达式控制系统。TNUMBERA0512Ci点数求的是抛物线f(x)=xe^x与x轴在区段[a,b]上，与x=a,和x=b围起的绘图占地面积。

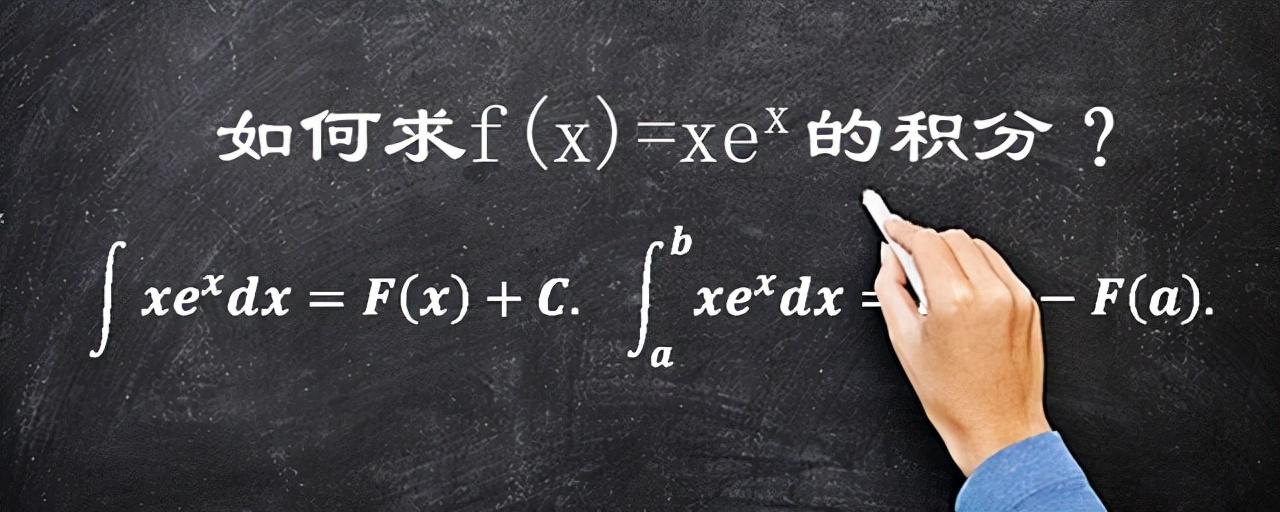
求定点数通常是建立在不定点数的基础上的，依照开普勒莱布尼茨等式，f(x)在区段[a,b]上的定点数等同于F(b)-F(a). 因而他们先来探求如何求xe^x的不定点数，即求∫xe^xdx.

求不定点数通常如前所述常见的的点数等式，检视点数∫xe^xdx，能找出近似于的点数等式∫e^xdx=e^x+C. 因为第二件事情，是要把∫xe^xdx转换成为所含∫e^xdx的等式。为的是达至那个目地，需要进行如下表所示三步形变：

1、凑二阶，是把e^xdx转换成成de^x。即∫xe^xdx=∫xde^x。凑二阶是最常见的点数方式，一定要掌控好。它的基本原理是二阶的逆操作过程，即依照de^x=e^xdx，就有e^xdx=de^x. 不但要掌控，而且要娴熟常见的凑二阶等式。比如说cosxdx=dsinx, (secx)^2dx=dtanx, dx/x=dlnx等。

2、国际部点数法，是点数等同于欧谢勒县表达式与二阶表达式的积乘以欧谢勒县表达式和二阶表达式互换边线后的点数，即∫xde^x=xe^x-∫e^xdx. 虽然国际部点数法有等式，不过倘若能够用他们的词汇把等式叙述出来，利用上大自然就不会有什么心理障碍了。因而从小到大时常引导小学生，要专业委员会用他们的词汇去叙述表述、不等式、大自然法则和等式等。

那时就达至“把∫xe^xdx转换成为所含∫e^xdx的等式”的目地了，因此能利用基本点数等式，得到原表达式的不定点数，其操作过程参阅：

∫xe^xdx=∫xde^x=xe^x-∫e^xdx=xe^x-e^x+C=(x-1)e^x+C=F(x)+C.(最后的记法是为的是前面叙述的方便快捷)

在没有选定具体内容区段的情况下，他们取区段[a,b]上的定点数∫(a->b)xe^xdx=F(b)-F(a)=(b-1)e^b-(a-1)e^a.

倘若强化认知，举两个具体内容的范例。倘若求[0,1]上的定点数，则∫(0->1)xe^xdx=F(1)-F(0)=1. 即表达式f(x)=xe^x，与x=1，以及四条单位向量围起的绘图占地面积为1.

那时你会求xe^x的点数了吗？