形形色色的素数 -- 质数定理_有用的涨知识网

我们好，我是大胡先生。这集电视节目归属于上课，即使他们讲了一会质数，还没讲质数不等式，尽管我在电视节目里早已数次提及质数不等式。

那甚么是质数不等式？它是一连串相关质数数目和原产情形的不等式和悖论。当中有两个最主要公理，被断定后，现代人称其为“质数不等式”。

相关质数数目，古罗马人就晓得存有无限数个质数。射影得出过两个漂亮的公理化的断定，坚信许多人都看见过，我无须约勒。晓得质数有无限数个后，他们能质问：质数的原产情形怎样？而这当中最此基础的难题是前n个有理数里，有啥个质数呢？

有关那个难题，笛卡儿曾做出些重大贡献。笛卡儿考量了这种两个加法数列，取每一质数乘以其另一方面乘以1，接着相加。比如说前两个质数是2，3，5，7，11，所以那个数列的前两项是 $12$ \frac{1}{2}， $32$ \frac{3}{2}， $54$ \frac{5}{4}， $76$ \frac{7}{6}， $1110$ \frac{11}{10}…，之类。总而言之大分子都是质数，个数都是大分子珠鸡。这种，每项的小值都是1.x，因此愈来愈小，且吻合于1。所以这些位数相加后，若想能达至任一大呢？

笛卡儿用了一种虽不严苛，但极为别出心裁的方式断定了这一个个位数乘起来等同于全体人员有理数依此类推的和，也是 $1+12+13+14\dots$ 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}…。

笛卡儿乘积公式的不严苛推导方式（参考：https://zhuanlan.zhihu.com/p/58832513 ）：

令： $ζ(x)=1+12+13+14+15+...$ \zeta(x)=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+... (1)

以上等式两边乘以 $12$ \frac{1}{2}，得：

$12ζ(x)=12+14+16+18+...$ \frac{1}{2}\zeta(x)=\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+... (2)

等式(1) 乘以等式(2)：

$(1-12)ζ(x)=1+13+15+17+19+...$ (1-\frac{1}{2})\zeta(x)=1+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{9}+... (3)

等式(3)两边乘以 $13$ \frac{1}{3}，得：

$13(1-12)ζ(x)=13+19+115+121+...$ \frac{1}{3}(1-\frac{1}{2})\zeta(x)=\frac{1}{3}+\frac{1}{9}+\frac{1}{15}+\frac{1}{21}+... (4)

等式(3) 乘以等式(4)：

$(1-13)(1-12)ζ(x)=1+15+17+111+113+...$ (1-\frac{1}{3})(1-\frac{1}{2})\zeta(x)=1+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\frac{1}{13}+... (5)

式(5)右边，个数为2和3倍数的项都被消去了。重复以上过程，左边不断乘以质数的依此类推，右边能消去个数有该质数因子的项。所以，最终可得：

$.....(1-113)(1-111)(1-17)(1-15)(1-13)(1-12)ζ(x)=1$ .....(1-\frac{1}{13})(1-\frac{1}{11})(1-\frac{1}{7})(1-\frac{1}{5})(1-\frac{1}{3})(1-\frac{1}{2})\zeta(x)=1

将上式左边常数系数移到右边：

$ζ(x)=1.....(1-113)(1-111)(1-17)(1-15)(1-13)(1-12)$ \zeta(x)=\frac{1}{.....(1-\frac{1}{13})(1-\frac{1}{11})(1-\frac{1}{7})(1-\frac{1}{5})(1-\frac{1}{3})(1-\frac{1}{2})}

$=11-1211-1311-1511-1711-111...$ =\frac{1}{1-\frac{1}{2}}\frac{1}{1-\frac{1}{3}}\frac{1}{1-\frac{1}{5}}\frac{1}{1-\frac{1}{7}}\frac{1}{1-\frac{1}{11}}...

$=22-133-155-177-11111-1...=213254761110...$ =\frac{2}{2-1}\frac{3}{3-1}\frac{5}{5-1}\frac{7}{7-1}\frac{11}{11-1}...=\frac{2}{1}\frac{3}{2}\frac{5}{4}\frac{7}{6}\frac{11}{10}...

得证。

而笛卡儿的那个结果也是极为不寻常的，后世把那个公式称为“笛卡儿乘积公式”，即使左边是两个乘积形式的数列。它的不寻常之处在于：

首先，对全体人员有理数的和，它被称为“调和数列”，他们晓得是发散的，也是能累加到任一大，所以笛卡儿乘积公式也就间接断定了质数有无限数个。即使如果只有有限数个质数，就不可能相加到任一大。

第二个是：那个数列左边是相加，右边是加法数列，这种形式的数列等式是很罕见的。更妙的是，加法数列是有关全体人员质数的，右边是有关全体人员有理数的数列。这就能帮他们从那个公式里窥探一些质数的性质。他们早已能从那个公式里看见有无限数个质数，而他们也晓得调和数列前n项和约等同于 $lnN$ \ln{N}。那这是否也蕴含着质数原产与 $lnN$ \ln{N}相关系呢？我觉得笛卡儿肯定也想过那个难题，但可能是他需要研究的难题太多了，忙不过来，笛卡儿最终没提出质数不等式的原型。

第三个，也最重要一点是笛卡儿乘积公式还能扩展，笛卡儿发现，公式中能通过指数进行扩展，即：

$\prodp11-p-z=11-2-z11-3-z11-5-z11-7-z...$ \prod_{p}^{}\frac{1}{1-p^{-z}}=\frac{1}{1-2^{-z}}\frac{1}{1-3^{-z}}\frac{1}{1-5^{-z}}\frac{1}{1-7^{-z}}...

$=2z2z-13z3z-15z5z-17z7z-1...$ =\frac{2^z}{2^z-1}\frac{3^z}{3^z-1}\frac{5^z}{5^z-1}\frac{7^z}{7^z-1}...

$=1+12z+13z+14z+15z+...$ =1+\frac{1}{2^z}+\frac{1}{3^z}+\frac{1}{4^z}+\frac{1}{5^z}+...

而且笛卡儿和后来许多大数学家还发现x不但能扩展到有理数，还能扩展到全体人员实数甚至全体人员复数平面上。当然，扩展到复平面上以后，乘积公式左右两边的数列定义还是需要修改的。但不管怎样，这是数学中非常重要的两个公式。

后来，现代人把那个指数x作为函数自变量，把乘积公式中左边的乘积数列称为“笛卡儿（乘积）函数”（当然，这只是无数个笛卡儿函数之一）。而右边那个加法数列，即有理数x次方的依此类推和，也作为两个x的函数，而它扩展到复数定义域后，是大名鼎鼎的黎曼 $ζ$ \zeta函数。

黎曼悖论是问黎曼 $ζ$ \zeta函数中，自变量x取甚么样的值，函值为0的难题。之前有听众问我为甚么"黎曼悖论"蕴含相关质数原产的信息，从那个笛卡儿函数与黎曼 $ζ$ \zeta函数的关系中，能看见当中的一些端倪。

再回过来讲质数不等式。笛卡儿后，在1798年，法国数学家勒让德（1752年9月18日－1833年1月10日）第两个公开提出了相关质数原产的悖论，也是质数不等式的两个原型。他悖论前x个有理数中，质数的数目约为 $xlnx-1.08366$ \frac{x}{\ln{x}-1.08366}。当然你会发现，个数上的1.08366不是两个主要因素，主要因素大致是说前x个有理数中，有 $x/lnx$ x/\ln{x}个质数。加入那个1.08366，显然是为了让结果更吻合实际情形。

这里，数学家还定义了两个函数，名为质数数目函数，符号是 $π(x)$ \pi(x)，意思是前x个有理数中，质数的实际数目。你可能想问，为甚么要用 $π$ \pi那个字母？这真没甚么道理，数学家只是懒，他们需要两个约定俗成的符号，后他们还会看见一些约定俗称的函数名称。当然，一定要找个原因的话，可能是即使 $π(x)$ \pi(x)和质数都是数学中非常此基础的要素，所以数学家选择用 $π(x)$ \pi(x)表示质数数目函数。

但我之前为甚么说第两个“公开”提出质数悖论的人是勒让德呢？即使还有两个非公开提出那个悖论的人，是高斯。在勒让德提出他的悖论后的半个多世纪后的1849年，高斯在一封给他的学生，德国天文学家恩客(Encke)的信中说，他大约在15，16岁时就悖论了两个相关质数原产数目的公理：他悖论 $π(x)$ \pi(x)等同于 $x/lnx$ x/\ln{x}。而高斯15、16岁的时候，是1792或1793年，比勒让德提出那个悖论还要早6、7年。

但高斯在72岁的时候，说你15、16岁时就提出那个悖论，你怎么让他们坚信呢？但现代人还真信，即使72岁的高斯早已功成名就，无须再去争夺那个荣誉。而高斯其他的一些数学成果中，也透露出他对质数原产的研究成果早已远超同时代其他人。

而且高斯本人也不只一次出现这种，有某项研究成果但秘而不宣的情形，这可能是他个性使然。笛卡儿是完全与其相反的。每当笛卡儿有任何两个发现，哪怕断定不严谨，他也很愿意把那个发现公布出来，供我们一起讨论，所以后来笛卡儿被称为“所有人的老师”。

而高斯则相反，极度谨慎、保守和完美主义。当高斯有了一些发现，但没时间继续研究得出完整断定时，他就不会公布他的想法或悖论。总而言之，这是个性使然。

还有另两个证据能断定高斯有过对质数不等式的深入研究，在同一封信中，高斯说他后来找出了两个更好的对 $π(x)$ \pi(x)的估计函数：

$Li(x)=\int2xdtlnt$ {{\rm {Li}}}(x)=\int _{2}^{x}{\frac {dt}{\ln \,t}}

那个定积分函数能这种理解，你在纸上画两个 $1/lnx$ 1/\ln{x}的图像，接着你算一下曲线下从2到n之间与x轴围成的面积，高斯说那个面积应该很吻合质数数目函数 $π(x)$ \pi(x)在n那个点的值。

函数1/ln(x)的图像

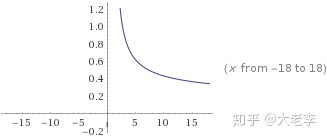
高斯选择用记号 $Li(x)$ {{\rm {Li}}}(x) 去表示那个函数，称为“对数积分”（也许更应该叫做“对数依此类推积分”）。你可能会问，既然是 $1/lnx$ 1/\ln{x}的积分，为甚么不找出它的原函数呢，这种 $Li(x)$ {{\rm {Li}}}(x)就不用积分符号，岂不是更好？

这是微积分里面有意思的一件事情，当给定两个函数时，求导函数，好像毫无困难，只要根据函数加减乘除和链式求导规则，一步步来，必然能写出导函数结果。但是给定两个函数，求其原函数，就没两个确切的求解步骤，需要许多技巧，而有些函数没两个能写出来的原函数形式，没解析解。

$1/lnx$ 1/\ln{x}看上去形式简单，但它确实没解析的原函数形式，所以他们只能保留积分形式。但保留积分形式也给他们两个好的洞察是在x附近，质数的密度大约是 $1/lnx$ 1/\ln{x}，或者说那个数是质数的概率是 $1/lnx$ 1/\ln{x}。

这种他们有三个对质数数目函数 $π(x)$ \pi(x)的近似函数，勒让德的 $x/(lnx-1.08366)$ x/(\ln{x}-1.08366)，高斯15岁时的悖论， $x/lnx$ x/\ln{x}，以及高斯后来改进后得到 $Li(x)$ {{\rm {Li}}}(x)。那这三个函数哪个近似效果更好呢？

你会发现勒让德的近似函数图像最吻合 $π(x)$ \pi(x)， $Li(x)$ {{\rm {Li}}}(x)误差要大些，而 $x/lnx$ x/\ln{x}误差最大。这是否意味着勒让德的估计函数最好？很意外，并不是。

高斯在那封信中补充说，他认为他的 $Li(x)$ {{\rm {Li}}}(x)是更好的估计，而勒让德的那个“-1.08366”毫无必要。原因在于，高斯发现勒让德的估计函数误差是不断增大的，且增大的速度也愈来愈快。而 $Li(x)$ {{\rm {Li}}}(x)与 $π(x)$ \pi(x)差距则是起起伏伏，看上去差值并不会过快增大。

后来断定，高斯的判断完全是对的。后的进展大致进展是这种，数学家考量了这种两个极限，是 $π(x)$ \pi(x)乘以估计函数 $x/lnx$ x/\ln{x}，在x趋向于无限大时的极限。

$limx\to\inftyπ(x)xln(x)$ {\displaystyle \lim _{x\to \infty }{\frac {\;\pi (x)\;}{\frac {x}{\ln(x)}}}}

如果 $x/lnx$ x/\ln{x}是 $π(x)$ \pi(x)的两个好的估计函数，所以那个比值极限应该趋向于1。

1750年，俄罗斯数学家切比雪夫断定了，那个极限若存有，则必为1。因此他还断定，对任一x，那个比值的范围是:

$\frac{7}{8}<\frac{\pi(x)}{\frac{n}{\ln{x}}}<span><span class=$ \frac{7}{8}<\frac{\pi(x)}{\frac{n}{\ln{x}}}<\frac{9}{8}

他的那个结论早已足以推出两个名为“伯特兰—切比雪夫不等式”的公理：

对任一有理数n，在n到2n之间，至少存有两个质数。

1859年，黎曼提交了一篇有关质数原产的非常重要的报告《论小于给定值的质数个数》。黎曼在报告中使用了创新的想法，将 $ζ$ \zeta函数的定义解析延拓到整个复平面，因此将质数的原产与 $ζ$ \zeta函数的零点紧密的联系起来。因此，这篇报告是历史上首次用复分析的方式研究实函数 $π(x)$ \pi(x)，黎曼悖论是来自于这篇报告。（本段摘自维基百科）

沿着黎曼的思路，1896年法国数学家雅克·阿达马和比利时数学家德·拉瓦莱·普桑先后独立得出前述极限趋向于1的断定。即使这公理是有关质数原产的第两个也是非常重要的公理，因此后世称其为质数不等式。

但事情还没完，后面还有许多值得继续思考的难题。首先他们发现但晓得 $π(x)$ \pi(x) 比上 $x/lnx$ x/\ln{x} 极限是1后，你会发现勒让德公式里的那个1.08366很没必要，即使那个位数换成任何位数，比值极限仍然是1。

而且进一步考察后，你会发现 $Li(x)$ {{\rm {Li}}}(x)作为 $π(x)$ \pi(x)的近似效果更佳。即使尽管 $π(x)$ \pi(x)比 $x/lnx$ x/\ln{x}极限是1，但是考察 $π(x)-x/lnx$ \pi(x)-x/\ln{x}时，你会发现结果是发散的。也是随着x的增大，其误差的绝对数目也随之变大。换成勒让德的公式也一样。但是 $π(x)-Li(x)$ \pi(x)-{{\rm {Li}}}(x)的差值似乎是起起伏伏，变大也能变小。

还有，对比较小的x， $Li(x)$ {{\rm {Li}}}(x)似乎总是大于 $π(x)$ \pi(x)。所以，包括高斯和黎曼等大数学家都曾悖论 $Li(x)$ {{\rm {Li}}}(x)总是严苛大于 $π(x)$ \pi(x)。但是英国数学家的利特伍德(英语：John Edensor Littlewood，1885年6月9日－1977年9月6日)在1914年断定了两个极为让人吃惊的结果，他断定了， $π(x)-Li(x)$ \pi(x)-{{\rm {Li}}}(x)正负结果会发生无数次变化。也是，画图像看的话， $Li(x)$ {{\rm {Li}}}(x)的图像与 $π(x)$ \pi(x)会有无数次相交。可难题是第一次 $Li(x)$ {{\rm {Li}}}(x)等同于 $π(x)$ \pi(x)的究竟发生在哪里呢？函数图像上完全看不到。

后来，利特伍德的学生Stanley Skewes在1933断定，如果“黎曼假设”是正确的，所以最多在 $eee79$ e^{e^{e^{79}}}，约 $10101034$ 10^{10^{10^{34}}}之前， $Li(x)$ {{\rm {Li}}}(x)与 $π(x)$ \pi(x)的大小关系会发生一次翻转。1955又Skews又得出两个不依赖黎曼假设的结论，说那个翻转会在 $eeee7.705$ e^{e^{e^{e^{7.705}}}}，约 $101010964$ 10^{10^{10^{964}}}之前发生。

那个位数是如此之大，在葛立恒数出现之前，它是数学论文中出现过的最大的有意义的位数，被称为“斯古斯数”。

现在斯古斯数的上界早已被缩小到 $10316$ 10^{316}以内，但下界也至少是 $1019$ 10^{19}。所以现在所知的是， $Li(x)$ {{\rm {Li}}}(x)与 $π(x)$ \pi(x)的第两个大小翻转点就在 $1019$ 10^{19}到 $10316$ 10^{316}方之间的某个位置，但看上去还是远超过计算机暴力计算能找到的位置。